Spanning Tree
그래프 내의 모든 정점을 포함하면서 순환이 존재하지 않는 간선을 최소로 하는 최소 연결 부분 그래프를 의미합니다.
[간선의 수: n-1개, Cycle 존재 X]
Minimum Spanning Tree (MST)
특정 그래프의 Spanning Tree 중에서 간선들의 가중치의 합이 최소가 되는 Spanning Tree를 말합니다.
MST를 만드는 알고리즘은 대표적으로 크루스칼(Kruskal), 프림(Prim) 두 가지가 있습니다.
크루스칼 알고리즘
모든 간선을 가중치 기준으로 오름차순으로 정렬하고, 이 간선들을 순서대로 모든 정점이 연결될 때까지 연결하는 것입니다. 이 때 서로소 집합(disjoint set) 자료구조의 Union, Find 연산을 사용하여 순환(Cycle) 이 형성되지 않으면서 모든 정점을 연결할 수 있게 하여 MST를 만들 수 있습니다.
크루스칼 알고리즘 동작 방식
1. 그래프의 간선들을 가중치 기준 오름차순으로 정렬합니다.
2. 정렬된 간선 리스트를 순서대로 선택하여, 간선의 정점들을 연결합니다.
3. 이때 Union-Find의 Find를 활용하여 순환이 있는지 확인합니다.
4. 순환이 없다면, 정점을 연결하는 것은 Union-Find의 Union으로 구현합니다.
5. 위의 과정을 반복하여 최소 비용의 간선들만 이용하여 모든 정점이 연결됩니다.
크루스칼 알고리즘 동작 방식(그림)

간선의 가중치가 가장 작은 3, 6을 선택

다음으로 낮은 가중치의 1,2 와 2,5 선택

다음 낮은 가중치의 2,6 선택
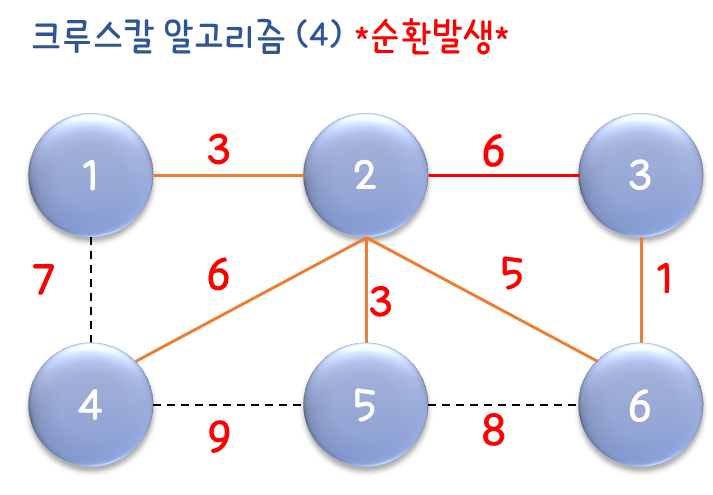
다음 낮은 가중치의 2,4 연결 2,3은 연결 시 순환이 발생

모든 정점이 연결된 최종 최소 스패닝 트리
크루스칼 알고리즘 구현
간선의 정보를 저장하기 위한 클래스 선언
static class Edge implements Comparable<Edge>{
int start; //출발 노드
int end; //도착 노드
int cost; //가중치
//생성자
public Edge(int start, int end, int cost) {
this.start = start;
this.end = end;
this.cost = cost;
}
//정렬을 할 때 비용을 기준으로 오름차순으로 정렬합니다.
@Override
public int compareTo(Edge o) {
return this.cost - o.cost;
}
}
간선 정보를 입력받고 List에 저장
BufferedReader br = new BufferedReader(new InputStreamReader(System.in)); //입력을 받기 위한 Buffer
StringTokenizer st = new StringTokenizer(br.readLine()); //한줄로 받은 입력을 띄어쓰기 기준으로 split
List<Edge> list = new ArrayList<>(); //간선 정보를 저장하기 위한 List 선언
for (int i = 0; i < e; i++) {
//정보를 한줄로 받기 (ex. 3 4 6 ...)
StringTokenizer st = new StringTokenizer(br.readLine());
//정보를 각각 변수에 저장
int start = Integer.parseInt(st.nextToken());
int end = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
//각 변수에 저장된 정보를 생성자를 사용하여 Edge 인스턴스를 생성하고 List에 저장
list.add(new Edge(start, end, cost));
}
//클래스를 선언할 때 compareTo에 따라 가중치를 기준으로 오름차순 정렬
Collections.sort(list);
간선의 리스트를 순서대로 선택하여 정점들을 연결 (Union-Find 활용)
static int[] parent; //union-find 연산시 필요한 int[] 선언
public static void main(String[] args) {
for (int i = 0; i < e; i++) {
Edge edge = list.get(i); //위에서 저장한 간선들의 정보를 하나씩 꺼내 edge에 저장
if(!isSameParent(edge.start, edge.end)){ //순환이 있는지 확인
union(edge.start, edge.end); //Union 연산을 사용하여 두 정점 연결
//result += edge.cost; *최소 가중치를 구해야하는 경우 result에 저장
}
}
}
private static int find(int x){
//자신의 노드의 최상위 부모 노드를 확인
if(parent[x] == x){
//현재 노드의 부모 노드가 자기 자신인지 확인
return x;
}
else {
//아니라면 find를 통해 최상위 부모 노드 찾기
return parent[x] = find(parent[x]);
}
}
private static void union(int start, int end) {
start = find(start); //각자 노드의 부모 노드를 확인
end = find(end);
if(start!=end){
//각자의 부모 노드가 같지 않다면 end노드의 부모노드를 start로 설정하여 두 정점을 연결
parent[end] = start; //end를 start에 연결
}
}
private static boolean isSameParent(int start, int end) {
start = find(start); //각자 노드의 부모 노드를 확인
end = find(end);
if(start==end) return true; //만약 같다면 순환(Cycle)이 생기므로 True를 return 한다.
else return false;
}크루스칼 알고리즘 시간 복잡도
크루스칼 알고리즘은 간선을 정렬하는데 O(ElogE)의 시간복잡도가 소요됩니다. 그리고 정렬된 간선을 순회하면서 UnionFind연산을 한번씩 수행합니다. 그렇기 때문에 O(1) * E 즉, O(E)의 시간복잡도가 발생합니다. 결과적으로 보면 O(ElogE + E)입니다. O(ElogE) = O(ElogV^2) = O(2*ElogV) = O(ElogV)가 됩니다.
크루스칼 알고리즘 특징
1. 간선 위주의 알고리즘입니다.
2. 순환(Cycle)이 이루어지는지 항상 확인하면서 트리를 구성해야 합니다.
3. 간선을 기준으로 정렬하는 과정이 오래 걸립니다.
4. 간선의 개수가 적은 경우에 크루스칼을 사용하는 것이 효과적입니다.
프림 알고리즘
시작 정점에서부터 출발하여 가중치가 적은 정점을 선택하여 연결하는 정점 기준으로 MST를 만드는 알고리즘입니다.프림 알고리즘에서는 Priority Queue를 활용하여 구현을 할 수 있습니다.
프림 알고리즘 동작 방식
1. 임의의 정점을 시작점으로 선택합니다.
2. 시작점에서 갈 수 있는 정점 중 가장 가중치가 작은 정점을 선택하여 연결합니다.
3. 연결된 정점에서 갈 수 있는 정점 중 가장 가중치가 작은 정점을 선택하여 연결합니다.
4. 위의 과정을 모든 정점이 연결될 때까지 반복을 하여 최소 비용으로 모든 정점을 연결합니다.
크루스칼 알고리즘 동작 방식(그림)

1과 연결된 2, 4 정점을 우선순위 큐에 삽입하고 2, 4중에 1,2가 가장 낮은 가중치를 갖고 있기 때문에 1, 2 연결

2와 연결된 3, 4, 5, 6 정점을 우선순위 큐에 삽입하고 우선순위 큐에 삽입된 정점 중에 2, 5가 가장 낮은 정점을 가지고 있으므로 2, 5 연결

5와 연결된 4, 6을 우선순위 큐에 삽입하고 우선순위 큐에 삽입된 정점 중에 2, 6이 제일 가중치가 낮으면서 6번 정점은 아직 방문하지 않았으니 2, 6 연결

6번과 연결된 3을 우선순위 큐에 삽입하고 우선순위 큐에 삽입된 정점 중에서 3번은 방문하지 않았고 6,3이 가중치가 가장 낮으므로 3, 6연결
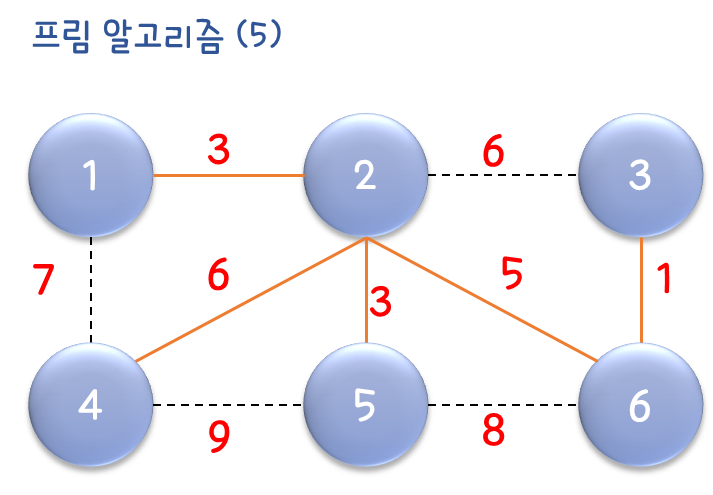
그리고 마지막으로 우선순위 큐에 삽입된 정점 중 방문하지 않고 가장 낮은 가중치를 갖고 있는 2, 4 연결
프림 알고리즘 구현
정점의 정보를 저장할 클래스 선언
static class Node implements Comparable<Node>{
int end; //도착 노드
int cost; //가중치
//생성자
public Node(int end, int cost) {
this.end = end;
this.cost = cost;
}
//정렬을 할 때 비용을 기준으로 오름차순으로 정렬합니다.
@Override
public int compareTo(Node o) {
return this.cost - o.cost;
}
}
정점 정보를 입력받고 List에 저장 ex. list[start_node].add(new(end_node, cost); 형태로 저장
List<Node>[] list = new ArrayList[v/*(노드의 개수)*/];
//리스트 배열 초기화
for (int i = 0; i < v; i++) {
list[i] = new ArrayList<>();
}
//정점 정보를 받아서 list에 저장
for (int i = 0; i < e; i++) {
st = new StringTokenizer(br.readLine());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
//방향이 없는 그래프로 가정하고 양뱡향으로 정보 저장
list[a].add(new Node(b, w));
list[b].add(new Node(a, w));
}
프림 알고리즘 구현
public static void main(String[] args) {
prim(1); //임의의 한 점에서 시작
System.out.println(total);
}
private static void prim(int start) {
//방문한 노드는 다시 방문하지 않기 위해 visited 배열 선언
boolean[] visited = new boolean[v/*(노드의 개수)*/];
//우선순위 큐 선언
Queue<Node> pq = new PriorityQueue<>();
//우선순위 큐에 임의로 정한 시작 노드와 가중치를 0으로 초기화해서 삽입
pq.add(new Node(start, 0));
//큐가 모두 비어질 때까지 반복
while (!pq.isEmpty()){
Node p = pq.poll();
int node = p.end;
int cost = p.cost;
//만약 node가 이미 방문한 노드라면 continue;
if(visited[node]) continue;
//방문하지 않은 노드라면 방문 처리를 해주고
visited[node] = true;
//result += cost; 최소비용을 구해야하는 경우 result에 가중치 증가
//해당 노드와 연결되어 있는 노드들을 꺼내서 방문하지 않은 노드가 있다면 우선순위 큐에 삽입
for (Node next : list[node]) {
if(!visited[next.to]){
pq.add(next);
}
}
//해당과정을 반복하면 최소 비용으로 연결된 트리를 구할 수 있다.
}
}프림 알고리즘 시간 복잡도
프림 알고리즘은 각 간선이 한 번씩 우선순위 큐에 삽입되고 제거됩니다. 이에 해당하는 시간 복잡도는 O(ElogE) 입니다.
프림 알고리즘 특징
1. 정점 위주의 알고리즘입니다.
2. 점점을 선택하면서 트리를 구성하기 때문에 순환(Cycle)이 발생하지 않습니다.
3. 최소 거리의 정점을 찾는 부분에서 자료구조의 성능에 영향을 받습니다.
4. 간선의 개수가 많은 경우에 프림을 사용하는 것이 효과적입니다.
[참고]
1. https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EA%B5%AC%EC%A1%B0
2. https://velog.io/@syc1013/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%B5%9C%EC%86%8C%EC%8B%A0%EC%9E%A5%ED%8A%B8%EB%A6%AC-Minimum-Spanning-Trees
3. https://ongveloper.tistory.com/376
4. https://velog.io/@fldfls/%EC%B5%9C%EC%86%8C-%EC%8B%A0%EC%9E%A5-%ED%8A%B8%EB%A6%AC-MST-%ED%81%AC%EB%A3%A8%EC%8A%A4%EC%B9%BC-%ED%94%84%EB%A6%BC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
5. https://godls036.tistory.com/26
'Algorithm' 카테고리의 다른 글
| [Algorithm] Greedy 알고리즘 _ 강의실 배정 (2) | 2022.10.21 |
|---|